$$ \newcommand{\lik}{\mathcal{L}} \newcommand{\X}{\mathbf{X}} \newcommand{\thetavec}{\mathbf{\Theta}} \newcommand{\likfun}{\mathcal{L}(\X|\thetavec)} \newcommand{\score}{s(\thetavec)} \newcommand{\finfo}{\mathcal{I}(\thetavec)} \newcommand{\vartx}{\underset{{X, \thetavec}}{\text{Var}}} \newcommand{\dodotheta}{\frac{\partial}{\partial \thetavec}} \newcommand{\EX}{\underset{\X}{\mathbf{E}}} $$ Calyampudi Radhakrishna Rao (కల్యంపూడి రాధాకృష్ణారావు) is a legendary mathematician and statistician who has made pioneering contributions to various fields such as information theory, estimation, inference, multivariate analysis, and orthogonal arrays. His groundbreaking work has had a profound impact on not only statistics butContinue reading “C.R Rao and his Lower Bound on Errors”
Category Archives: Math
Bayesian Estimates for the Parameters of a Power-law Distribution with Exponential Cutoff using Monte Carlo Methods
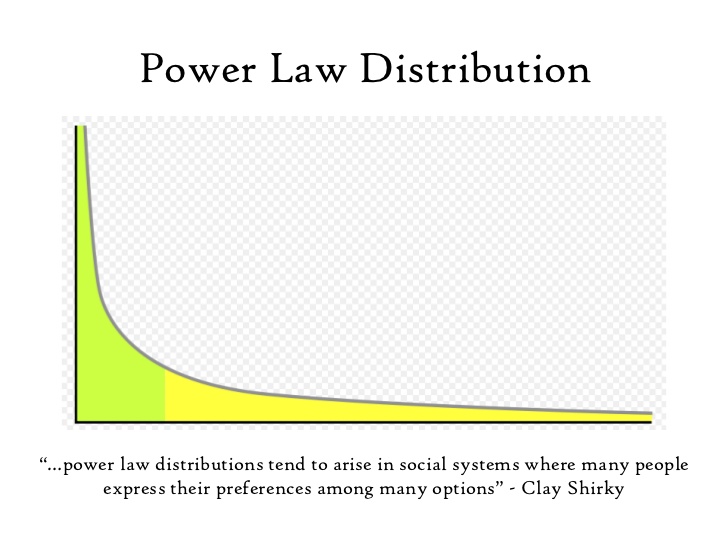
$$ \newcommand{\boldphi}{\boldsymbol{\phi}} \newcommand\xmin {x_{\text{min}}} \newcommand{\gammaone} {\Gamma_{\alpha}^{\prime} (1-\alpha, \lambda \xmin)} \newcommand{\gammatwo}{\Gamma_{\alpha}^{\prime \prime} (1-\alpha, \lambda \xmin)} \newcommand{\gammazero}{\Gamma (1-\alpha, \lambda \xmin)} $$ The power-law distribution is of the form $f(x) \propto x^{-\alpha}$, where $\alpha$ is called the scaling parameter. It models many natural phenomena like acoustic attenuation, Curie–Von Schweidler law, neuronal avalanches, and others. As $x \to 0$,Continue reading “Bayesian Estimates for the Parameters of a Power-law Distribution with Exponential Cutoff using Monte Carlo Methods”
Is the Dirichlet Function Riemann-Darboux Integrable?
The Dirichlet Function The Dirichlet function is one of the easiest functions to define. It’s literally, $$ \begin{aligned} f(x)=\left\{ \begin{array}{ll} 1, & \text{if $x$ is rational}\\ 0, & \text{if $x$ is irrational} \end{array} \right. \end{aligned} $$ or using the symbols from number theory/set theory that almost no one remembers, $$ \begin{aligned} f(x)=\left\{ \begin{array}{ll} 1, &Continue reading “Is the Dirichlet Function Riemann-Darboux Integrable?”
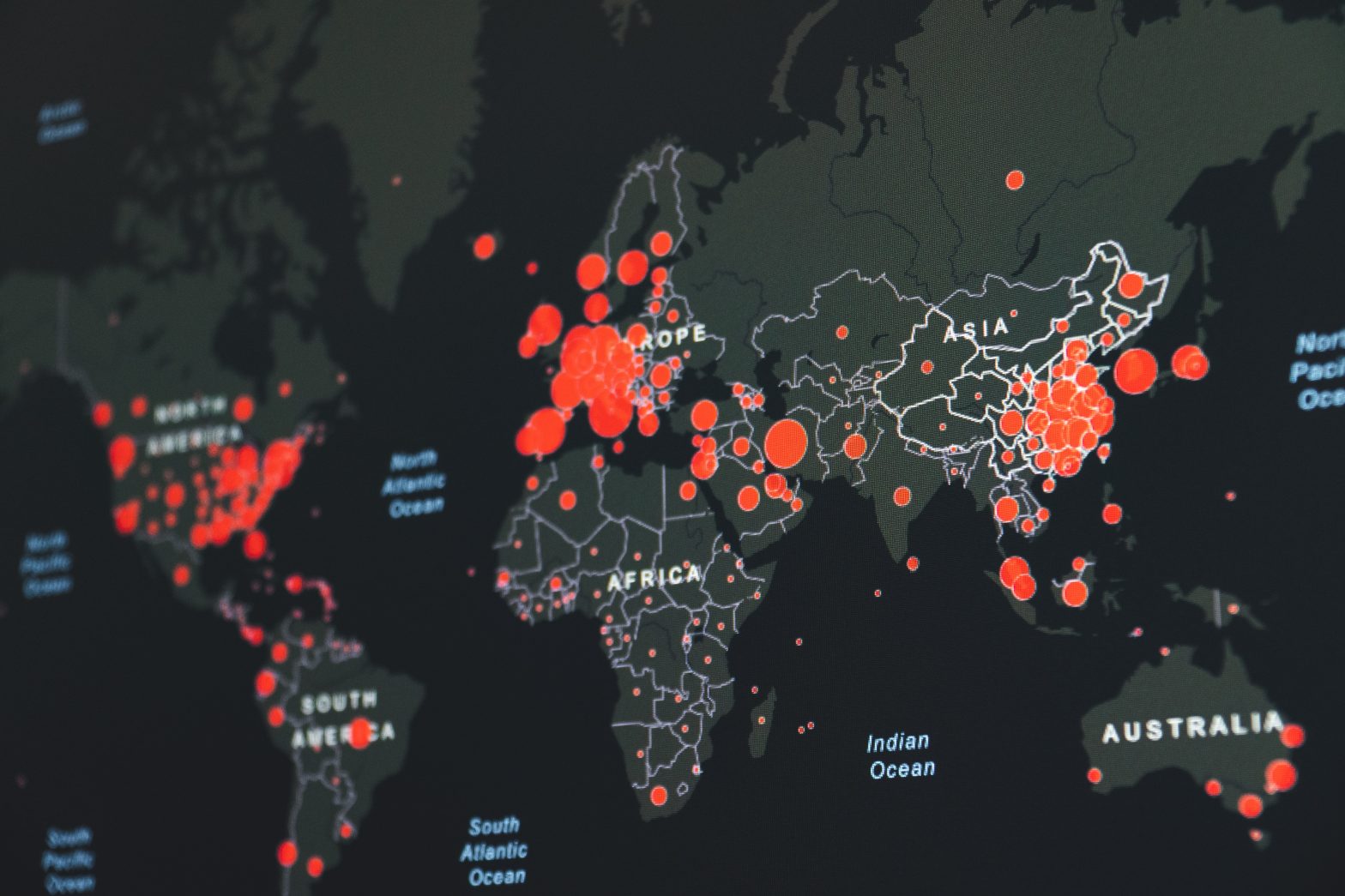
Bayesian Methods for the Estimation of Infection and Recovery Rates of an Epidemic from Stochastic SIR Data
This project was co-authored by Heather Johnston and Youngwoo Kwon $$ \newcommand{\boldphi}{\boldsymbol{\phi}} $$ Introduction COVID-19, or Coronavirus Disease 2019, was declared a pandemic by the World Health Organization on March 11, 2020. The disease originated in December 2019 in China and quickly spread around the world. Compared with the previous epidemics like Ebola and SARS,Continue reading “Bayesian Methods for the Estimation of Infection and Recovery Rates of an Epidemic from Stochastic SIR Data”
Analysis of Prevalence of Mental Illnesses and Suicide in Different Countries Using Gower Clustering Based Dimensionality Reduction of Growth Metrics and Simulation-Based Hypothesis Testing
Source code for this research: https://github.com/AnilBattalahalli/Analysis-Of-Mental-Illnesses Introduction In the last two decades, there have been significant developments in understanding the anatomy of the brain for mental illnesses like Major Depressive Disorder, Anxiety Disorder, Bipolar Disorder, Schizophrenia, Personality Disorder, etc. Most of these disorders, along with alcohol and drug abuse are studied together to analyze theContinue reading “Analysis of Prevalence of Mental Illnesses and Suicide in Different Countries Using Gower Clustering Based Dimensionality Reduction of Growth Metrics and Simulation-Based Hypothesis Testing”
Generation of Power Law Samples with Inverse Transform Sampling (Python, R and Julia)
Implementation of the Inverse Transform Sampling The probability density function of a power law distribution is given by, $$f(x\ | \ x_m,\alpha) = \frac{\alpha-1}{x_m} \left(\frac{x}{x_m}\right)^{-\alpha} \ , x>x_m$$ We can find the cumulative density function by, $$ \begin{aligned} F(x) &= \int_{-\infty}^x f(x\ | \ x_m,\alpha) \ dx\\ \\ &= \int_{-\infty}^x \frac{\alpha-1}{x_m} \left(\frac{x}{x_m}\right)^{-\alpha} I(x>x_m) \ dxContinue reading “Generation of Power Law Samples with Inverse Transform Sampling (Python, R and Julia)”